Hoy vengo a compartirles una técnica que acabo de aprender que creo es una combinación muy bella y “simple” de varias cosas de física y programación. Ilustra muuuuy bien la promesa de lo que sería la computación cuántica para resolver problemas NP-Completos o NP-Difíciles (más en unos momentos) y se llama “Quantum Annealing”.
Si alguien no se siente cómodo viendo ecuaciones, no se preocupe. Las puse para los math geeks y realmente no son el contenido principal.
Quantum Annealing por T. Kadowaki y H. Nishimoro
La naturaleza y la cuántica 101
Primero, hay que recordar que la naturaleza es floja. Cualquier sistema, si se le deja a su suerte, siempre buscará llegar al estado con menor energía posible gastando también la menor energía posible. Justo cómo el café que siempre lo vemos enfriarse y no calentarse.
El café tiene menor energía cuando está frío que cuando está caliente
¿Esto qué tiene que ver con la computación cuántica? Resulta que esto no sólo ocurre para sistemas “clásicos” como una taza de café, ¡sino que también ocurre para sistemas cuánticos!
No es necesario profundizar mucho, pero sí es necesario mencionar que las computadoras cuánticas funcionan a base de qubits en vez de bits. Un qubit es cualquier sistema (cuántico) que se pueda describir con dos estados. Uno de los ejemplos más simples es un electrón que puede ser un qubit porque su spin puede estar viendo hacia arriba 
o hacia abajo 
.
Esto se hace como analogía a los dos estados de un bit (de hecho, a los dos estados del qubit se les llama \(\ket{0}\) y \(\ket{1}\)), con la diferencia de que tenemos el poder de la superposición cuántica. Es decir, los qubits pueden ser 0 y 1 al mismo tiempo.
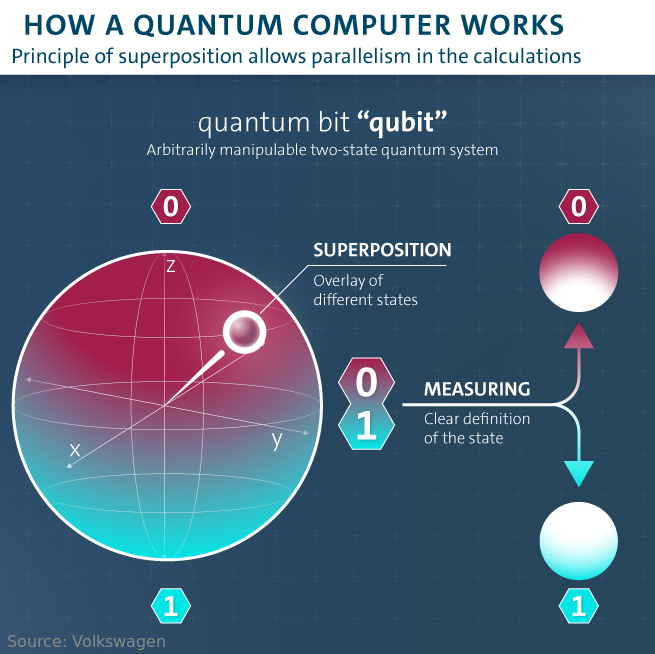¿Qué es un qubit? Imagen adaptada de Volkswagen
Por ejemplo, con 2 qubits tendrías al mismo tiempo todos los \(2^2\) estados posibles \(\ket{00},\ket{01},\ket{10},\ket{11}\) y puedes hacer operaciones con todos ellos de manera simultanea, en contraste con una computadora clásica que, para hacer esos mismos cálculos, tendría que hacerlos estado por estado.
⚛️ + Pereza = Quantum Annealing
Si combinamos el poder de la superposición con el caracter flojo de la naturaleza, podemos codificar problemas de minimización a un sistema cuántico y dejar que la naturaleza lo resuelva por nosotros haciendo que el estado con menor energía sea la solución al problema.
En otras palabras, si tenemos \(2^N\) estados posibles del cual nos interesa el más óptimo (ejemplo: de \(2^{10} \approx 1000\) rutas posibles, ¿cuál toma menos tiempo?), podemos codificar el problema en un sistema cuántico de tal forma que la energía represente al tiempo y dejar que la naturaleza solita encuentre el mínimo porque eso es lo que le gusta hacer. Además, como el sistema cuántico estará en superposición, no sería necesario revisar ruta por ruta sino que la naturaleza las revisaría todas al mismo tiempo.
Cómo lograr esto también tiene su belleza y mucha física metida y hacer ingeniería con eso es la parte bonita de la computación cuántica.
O sea, en términos más físicos…
Los grupos de spines de electrones (que justo mencionamos funcionan muy bien como qubits) ya los tenemos bien estudiados (le llamamos “Modelo de Ising”) y conocemos la ecuación para calcular su energía (le llamamos “el Hamiltoniano”), así que sólo faltaría aprender a codificar problemas en términos de estos spines para poder pedirle a la naturaleza que los resuelva.
Esto ya depende de cada problema, pero en el paper “Ising formulations of many NP problems” hay 27 páginas de ejemplos y ya abordaré uno más a detalle en otro artículo. Lo importante para conjuntar esta sección de física con la parte de programación (que pues resulta en computación cuántica jaja) es que los Modelos de Ising se pueden ver como grafos (que es otra forma de llamarle a las “redes” y que seguro son familiares para los que hayan estudiado computación) y son bien conocidos como problemas NP-Completos en el campo de programación lineal.
Como breviario cultural, en el argot de ciencias de la computación, los problemas:
- NP: son de decisión difíciles de resolver, pero fáciles de verificar una vez tenemos una solución.
- NP-Completos: son tales que pueden representar a cualquier otro de NP.
- NP-Difíciles: no son de decisión (pueden ser de optimización, por ejemplo), pero son tan difíciles de resolver como los NP.
En general, cualquier problema de optimización lo podemos traducir a uno de decisión si en vez de preguntar “¿cuál es el valor mínimo/máximo?”, preguntamos “¿existe algún valor menor/mayor que \(X\)?”. ¡Ahí está la importancia de todo esto! ¡Casi cualquier problema (i.e. casi cualquier pregunta) lo podemos resolver con un Modelo de Ising!
Las condiciones que definen a un problema las podemos meter al Hamiltoniano de Ising con multiplicadores de Lagrange (les resultará familiar a los que ya hayan trabajado con problemas de optimización pero, si no, no se preocupen. De nuevo, es para los math geeks) de tal forma que la energía mínima se dé cuando nuestra función objetivo sea minimizada y no hayan restricciones violadas. Es decir, cuando \(H(\vec{m})\) sea lo más cercana a cero.
Traducir eso a algo físico depende de cómo esté construida la computadora cuántica (puede ser con superconductores diminutos y campos magnéticos para manipular el spin), pero todos tienen algo en coḿun: la preparación del sistema. Ahí es donde entra el “annealing”.
¿Cómo se ve un qubit?
¿Qué es “annealing”?
La palabra “annealing” se traduce textualmente como “recocido” y se refiere al proceso de generar cristales (es decir, “estructuras”) lo más puros posibles a través de cambios de temperatura. Por ejemplo, este proceso se utiliza en la industria metalurgica para moldear piezas: primero se calienta el metal a temperaturas muy altas para poder darle forma y luego se enfría para que recupere su dureza (es decir, para “cristalizar”). Mientras más lento se haga el enfriamiento, menos impurezas tendrá el resultado y se tendrá una pieza más homogénea. Algo así es el proceso que se busca replicar a nivel cuántico.
Si encendemos la computadora cuántica y enfriamos a los super conductores para que exhiban propiedades cuánticas, los estaríamos poniendo en su estado de energía mínima (se le llama “estado base”). ¡Pero lo que nos interesa es el estado base de NUESTRO sistema (con todo y restricciones), no del sistema con el que enciende la computadora!
Físicamente, esta transformación se hace apagando gradualmente los campos magnéticos que bootearon a la computadora (que digamos están descritos por un Hamiltoniano \(H_0\)) e ir encendiendo a los que van a configurar a nuestro sistema (llamémoslos \(H_1\)) a un ritmo similar para, poco a poco, llevar a la computadora cuántica al sistema que nos interesa.
Este proceso se tiene que hacer muuuy despacio (en el argot físico se le llama “adiabáticamente”) para que el estado base del sistema inicial se convierta en el estado base de nuestro sistema (que recordemos es la solución) con la menor cantidad de ruido posible. Si se hiciera demasiado rápido, se correría el riesgo de que parte de esta energía sea transferida a los qubits y pasen del estado base a algún estado con mayor energía (es decir, un estado excitado) en los puntos donde se encuentren muy cercanos. Esto sería malo porque los estados excitados, al tener mayor energía, no son la solución más óptima a nuestro problema.
Como en cuántica todo es probabilístico y, según el gato de Schrödinger, el sistema decide en qué estado está hasta que lo observamos, si hacemos el proceso con mucho cuidado casi siempre veremos el estado base, pero podríamos ver algún otro una que otra vez. Sólo hay que ejecutar el programa varias veces hasta poder claramente discernir cuál aparece más y decir que ese es el que la naturaleza escoge con menor energía. Es decir, el estado base.
¡Y ya! 😃 Lo malo es que como el proceso debe ser adiabático, deberíamos ejecutarlo infinitamente despacio (literalmente) para obtener una solución 100% correcta. Hay algoritmos más nuevos (QAOA es uno muy en el state-of-art) que ofrecen un trade-off para poder solventar esa restricción, pero eso será tema para otra ocasión.